Besides sphere and plane intersections another important one is the ray / triangle intersection, because most 3D models consist of triangles or can be converted to such a representation. So let’s learn how to do it to be able to model some complex models.

A triangle $$T$$ can be represented by three points $$v0, v1, v2$$ that define a plane. So first, we check if the ray intersects this plane. I already did a tutorial on ray / plane intersection so I won’t cover it again. If there is such an intersection it means we just have to check if this hitpoint $$P$$ lies within the bounds of the triangle. For this we calculate a different representation of $$P$$ with respect to the triangle: As the point is on the plane, it can be written as $$P = v0 + su + tv$$ for some $$s,t$$ where $$u$$ and $$v$$ are the “edge vectors” incident to $$v0$$.

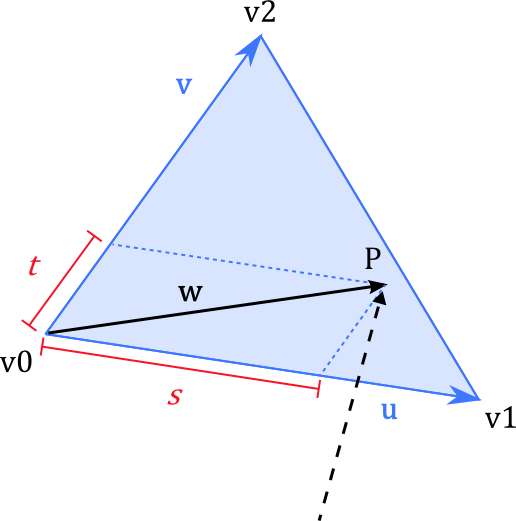
Once we have found the values for $$s,t$$ the following has to be true for the point to be inside the triangle:

1. $$0 \leq s,t \leq 1$$
2. $$s + t \leq 1$$

These constraints on $$s,t$$ essentially define the triangle structure and all in all, the set of points of the triangle is $$ \begin{aligned} T = {P \mid & P \in T_{\text{Plane}} \land P = v0 + s(v1-v0) + t(v2-v0) \land \\ & 0 \leq s,t, \leq 1 \land s + t \leq 1} \end{aligned}$$

Assume we have checked that $$P$$ lies inside the triangle’s plane, then we just have to solve $$P = v0 + su + tv$$ for $$s,t$$, or equivalent $$w = P - v0 = su + tv$$.

Solving the equation

Unfortunately, $$w = su + tv$$ has two unknowns ($$s,t$$) in only one equation, so we have to use a little trick to get two equations out of this. The normal $$n$$ of the triangle can be computed by the cross product of $$u$$ and $$v$$. Let’s now consider the vector $$u^\perp$$ that is both perpendicular to $$u$$ and to $$n$$. This vector lies in the plane and can again be computed by using the cross product, i.e., $$u^\perp = n \times u$$. We can now (dot product-) multiply our equation $$w = su + tv$$ on both sides by $$u^\perp$$:

$$ \begin{aligned} w = su + tv \\ w \cdot u^\perp = s u \cdot u^\perp + t v \cdot u^\perp \\ w \cdot u^\perp = t v \cdot u^\perp \end{aligned} $$

The term $$u \cdot u^\perp$$ is $$0$$, because by definition of $$u^\perp$$ it is perpendicular to $$u$$, and with it the $$s$$ vanishes and we have reduced the equation to only one unknown, so we solve it for $$t$$ by:

$$ \begin{aligned} t = \frac{w \cdot u^\perp}{v \cdot u^\perp} \end{aligned} $$

We do a similar thing to compute $$s$$ by multiplying with $$v^\perp = n \times v$$: $$ \begin{aligned} w = su + tv \\ w \cdot v^\perp = s u \cdot v^\perp + t v \cdot v^\perp \\ w \cdot v^\perp = s u \cdot v^\perp \\ s = \frac{w \cdot v^\perp}{u \cdot v^\perp} \end{aligned} $$

Some optimizations

We can reduce the number of computations by seeing that the denominator used to compute $$s$$ is just the negative of the denominator for $$t$$:$$u\cdot v^\perp = u \cdot (n \times v) = v \cdot (u \times n) = v \cdot (-n \times u) = - v \cdot (n \times u) = - v \cdot u^\perp$$ This gives us the following equations:

$$\begin{aligned} s = \frac{w \cdot v^\perp}{u \cdot v^\perp} && v^\perp = n \times v && w = P - v0 \\ t = \frac{w \cdot u^\perp}{-u \cdot v^\perp} && u^\perp = n \times u & \end{aligned}$$

In the case of raytracing where we shoot a ray through the scene for every pixel, we can save a lot of computation time by caching some of these values. In fact, the only term that depends on the ray is $$w$$, whereas $$u^\perp, v^\perp, u \cdot v^\perp$$ only have to be computed once for each triangle.

Here’s some C# code that implements the ray/triangle intersection test:

using UnityEngine;

public class RTTriangle : RTObject
{
    protected Vector3 v0, v1, v2;
    protected Vector3 normal;
    protected Vector3 u, v;
    protected Vector3 uPerp, vPerp;
    protected float denominatorST;

    public RTTriangle(Vector3 v0, Vector3 v1, Vector3 v2, bool clockwise = false)
    {
        Init(v0, v1, v2, clockwise);
    }
    
    protected void Init(Vector3 v0, Vector3 v1, Vector3 v2, bool clockwise = false)
    {
        this.v0 = v0;
        this.v1 = v1;
        this.v2 = v2;
        u = v1 - v0;
        v = v2 - v0;

        // Unity uses clockwise winding order to determine front-facing triangles
        // Unity uses a left-handed coordinate system
        // the normal will face the front
        // if the direction of the normal is not important to you
        // just remove the clockwise branching
        normal = (clockwise ? 1 : -1) * Vector3.Cross(u, v).normalized;

        uPerp = Vector3.Cross(normal, u);
        vPerp = Vector3.Cross(normal, v);
        denominatorST = Vector3.Dot(u, vPerp);
        if (Mathf.Abs(denominatorST) < Mathf.Epsilon)
        {
            Debug.LogError("Triangle is broken");
            return;
        }
    }

    public override RayTracer.HitInfo Intersect(Ray ray)
    {
        RayTracer.HitInfo info = new RayTracer.HitInfo();

        Vector3 d = ray.direction;
        float denominator = Vector3.Dot(d, normal);

        if (Mathf.Abs(denominator) < Mathf.Epsilon) return info;      // direction and plane parallel, no intersection

        float tHit = Vector3.Dot(v0 - ray.origin, normal) / denominator;
        if (tHit < 0) return info;    // plane behind ray's origin

        // we have a hit point with the triangle's plane
        Vector3 w = ray.GetPoint(tHit) - v0;

        float s = Vector3.Dot(w, vPerp) / denominatorST;
        if (s < 0 || s > 1) return info;    // won't be inside triangle

        float t = Vector3.Dot(w, uPerp) / -denominatorST;
        if (t >= 0 && (s + t) <= 1)
        {
            info.time = tHit;
            info.hitPoint = ray.GetPoint(tHit);
            info.normal = normal;
        }

        return info;
    }
}

You can now import a 3D model consisting of triangles in .obj format, parse the triangles and do your ray test. This is what the result might look like, a lot better than just planes and spheres.